Requirements for the Major or Minor

Requirements for the Major in Mathematics

Number of Units

Nine units of mathematics are required, exclusive of SIP and CS/Applied Statistics Cognate. Typically up to two units from outside courses (AP, transfer, dual enrollment, or study abroad) may count towards the major or minor in mathematics. MATH 260 and 261 do not count for the major. Students who wish to apply additional external units toward the major must consult with the department.

For purposes of course placement and prerequisites, a score of 4 or 5 on the AB calculus exam (or AB subscore of BC calculus exam) will be awarded credit equivalent to MATH 112.   A score of 4 or 5 on the BC Calculus exam is equivalent to MATH 113.  A score of 4 or 5 on the statistics exam is equivalent to MATH 260.  (MATH 260 cannot be counted towards the major or minor in mathematics.  A score of 3 or higher on the AP statistics exam may be used to satisfy the MATH 260 prerequisite for MATH 360.) As the department does not offer a precalculus course, no Kalamazoo College credit is awarded for the AP precalculus exam.

Required Courses

  • MATH 112-113 Calculus I and II
  • MATH 214 Calculus III
  • MATH 240 Linear Algebra and Vectors
  • MATH 310 Complex and Vector Variables, MATH 316 Topics in Number Theory, or MATH 318 Topics in Topology
  • MATH 320 Real Analysis I or MATH 330 Abstract Algebra I
  • One two-term sequence beyond calculus (e.g., Real Analysis I and II, Abstract Algebra I and II, Probability and Mathematical Statistics, Abstract Algebra I and Linear Algebra II)

Among the courses we offer, MATH 320 and MATH 330 are at the highest level of abstraction. Before enrolling in on eof these courses, students are strongly encouraged to complete MATH 310, 316, or 318.

For students interested in graduate work in one of the mathematical sciences, additional work in MATH 280, 310, 316, 318, 320, 330, 420, 430, and 450 is appropriate. Those with a strong interest in computing should elect the minor in computer science in addition to MATH 300. For those students interested in applied work (mathematical biology, mathematical economics, operations research, etc.), election of MATH 270, 280, 305, 310, 362, 365, 440, and at least two units in computer science is appropriate. Other departments offer classes that use mathematical ideas: BIOL 112, 426, and 436; CHEM 310 and 410; ECON  305 and 412; PHIL 107; PHYS 340, 400, 410, and 420; and PSYC 390.

Course descriptions are listed here.

Required Cognate

One unit of computer science or one applied statistics course (MATH 260 or 261).

In order to graduate with a major in mathematics a student must, in addition to the regular course requirements:

  • Pass the sophomore comprehensive exercise at the completion of Calculus I, II, III, and Linear Algebra (also referred to as the New Majors Math Exercise)
  • Pass the senior comprehensive exercise (more details will be provided during Winter term)
  • Complete the math colloquium credit (also referred to as MC2)

Senior Seminar Requirement

There may not be a senior seminar in mathematics during any given year.  When that occurs, students pursuing a major in mathematics fulfill their senior seminar requirement either (1) by completing a senior seminar offered by another department in which they are also pursuing a major or (2) by completing an interdisciplinary senior seminar.

Honors in the Major

Conferral of honors in the major falls entirely within the purview of the department.  In order to qualify for honors in the major, a math student must be judged by the faculty to meet the following two criteria: (1) honors level GPA in coursework in mathematics (GPA at least 3.75) and (2) either honors on a SIP in mathematics or exceptional breadth and depth of involvement in the department as reflected in coursework and activities.

Study Abroad

Students interested in mathematics are especially encouraged to consider the study abroad program in Budapest. The Budapest program is given in English; no prior knowledge of Hungarian is needed. It offers a number of mathematics courses as well as history, language, and literature courses. Mathematics majors have also studied mathematics in Erlangen, Quito, Perth, Aberdeen, and Lancaster. Early consultation with the department is strongly urged. 

Requirements for the Minor in Mathematics

There are four options for the minor in mathematics, each of which requires six units of credit in mathematics. Each of these options requires the “core” courses: Single variable calculus (MATH 112 and MATH 113), Multivariable Calculus (MATH 214), and Linear Algebra (MATH 240). The other required courses for each  option are as follows:

  • Statistics Option: MATH 362 Probability & MATH 365 Mathematical Statistics
  • Computational Mathematics Option: One of MATH 250 Discrete Mathematics or MATH 330 Abstract Algebra I and MATH 300 Automata, Formal Languages, and Computability
  • Applied Mathematics Option: MATH 280 Differential Equations and MATH 310 Complex and Vector
  • Pure Mathematics Option: One of MATH 320 Real Analysis I or MATH 330 Abstract Algebra I and one other mathematics course from the following list: MATH 310, MATH 316, MATH 318, MATH 320, MATH 330, MATH 362, or any 400-level course

Recommended Course Sequence for Majors

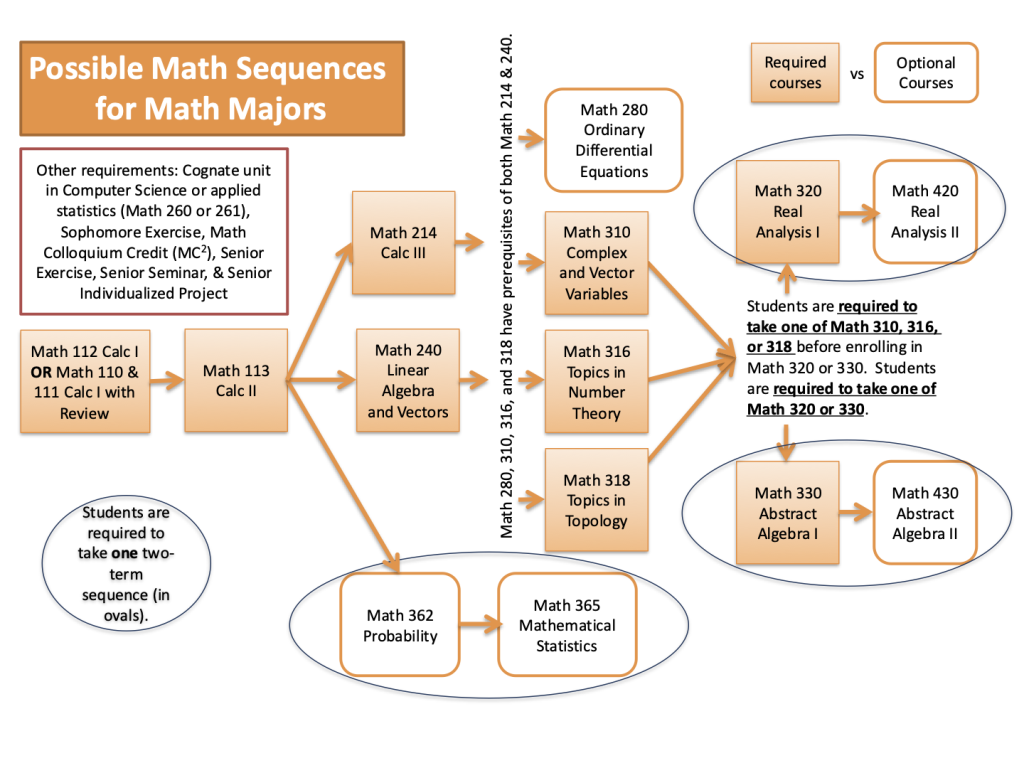
Flowchart of math course sequence for majors, described below.
  1. Math 112 Calc I OR Math 110 and 111 Calc I with Review
  2. Math 113 Calc II
  3. Math 214 Calc III and Math 240 Linear Algebra and Vectors
  4. Choose one (prerequisites are both Math 214 and 240):
    1. Math 310 Complex and Vector Variables
    2. Math 316 Topics in Number Theory
    3. Math 318 Topics in Topology
  5. Choose one (prerequisite is one of Math 310, 316, or 318):
    1. Math 320 Real Analysis I
    2. Math 330 Abstract Algebra I
  6. Choose one two-term sequence beyond calculus
    1. Math 362 Probability and Math 365 Mathematical Statistics
    2. Math 320 Real Analysis I and Math 420 Real Analysis II
    3. Math 330 Abstract Algebra I and Math 430 Abstract Algebra II